| Ultimate Fractal
|
 |
| Over Fractals |
| De Mandelbrotverzameling |
| Juliaverzamelingen |
| Newtonverzamelingen |
| Waar te beginnen |
| Fractal Parameters |
| In en uitzoomen |
| Kleuren |
| Het menu Bestand |
| Het menu Bewerken |
| Het menu Beeld |
| Het menu Opties |
| Het menu Help |
 |
|
Over Fractals
|
| Een fractal is een meetkundig figuur dat op elke schaal onregelmatig is. Fractals hebben een oneindige hoeveelheid details, en bij sommige fractals komen motieven voor die zich op steeds kleinere schaal herhalen. Doorgaans kunnen fractals gegenereerd worden door het herhaald toepassen van een bepaalde (wiskundige) bewerking. De term fractal werd geïntroduceerd in 1975 door Benoît Mandelbrot, afgeleid van het Latijnse fractus (gebroken). |
 |
| Meer informatie over fractals
|
 |
 |
 |
 |
 |
| De Mandelbrotverzameling is een beroemd voorbeeld van een fractal. |
|
De Mandelbrotverzameling van dichterbij bekeken. |
|
 |
| De Mandelbrotverzameling
|
| De Mandelbrotverzameling is een fractal die een belangrijke rol speelt in de chaostheorie. De verzameling is vernoemd naar Benoît Mandelbrot, een Pools-Franse wiskundige die de fractal in 1980 voor het eerst met de behulp van een computer onderzocht. Buiten de chaostheorie staat de Mandelbrotverzameling vooral bekend om zijn esthetische eigenschappen. Het is zeer de moeite waard om op de verzameling in te zoomen: je weet nooit wat je zult tegenkomen. De Mandelbrotverzameling wordt gegenereerd door de formule:zn+1 = zn2 + c waar z en c complexe getallen zijn: z = x + iy, z0 = 0 en c is een punt in het complexe vlak. De formule is afgelopen wanneer |zn| (de lengte van z) groter of gelijk is aan de bailout waarde van 2. De pixel die overeenkomt met c wordt afhankelijk van het aantal iteraties die zich hebben voorgedaan ingekleurd. De oninteressante zwarte gebieden van de afbeelding is de eigenlijke Mandelbrotverzameling. Het bestaat uit alle waarden van c waarvoor |zn| nooit groter wordt dan 2. Het is natuurlijk onmogelijk om dit gebied nauwkeurig te berekenen, dus zal het programma de kleur zwart toekennen aan alle pixels waarvoor |zn| nooit groter wordt dan 2 voor een opgegeven aantal maximum iteraties, bijvoorbeeld 256. De Kubische Mandelbrotverzameling wordt gegenereerd door de formule: zn+1 = zn3 + c De Kwadratische Mandelbrotverzameling wordt gegenereerd door de formule: zn+1 = zn4 + c
|
 |
| Meer informatie over de Mandelbrotverzameling
|
 |
 |
 |
 |
 |
| De Kubische Mandelbrotverzameling |
|
De Kwadratische Mandelbrotverzameling |
|
 |
| Juliaverzamelingen
|
| Een van de meest basale fractal types is de familie van Juliaverzamelingen, die door de Franse wiskundige Gaston Julia tijdens de Eerste Wereldoorlog werd ontdekt. Juliaverzamelingen worden berekend aan de hand van een simpele formule met een complexe parameter genaamd C. Door deze parameter te variëren kunnen vele verschillende fractals worden gegenereerd. Ook bij Juliaverzamelingen komen motieven voor die zich op steeds kleinere schaal herhalen.
|
 |
| Meer informatie over Juliaverzamelingen
|
 |
 |
| Juliaverzameling voor C = [-0.4, 0.6]. |
 |
| Newtonverzamelingen
|
| Deze fractal wordt gemaakt door de vergelijking z3 = 1 op te lossen met behulp van de Newton-Raphson methode, waarbij z een complex getal is: z = x + iy. Door het definiëren van de functie p(z) = z3 - 1, en door deze te gebruiken in een iteratieve formule die moeten convergeren naar nul vindt men een waarde van z als oplossing voor de vergelijking. Een algemene formule voor de Newton iteratie is:zn+1 = zn - a * p(zn) / p'(zn) Waar a een complex getal is en p'(z) de afgeleide is van p(z). De speciale waarde a = 1 komt overeen met de Newton fractal. De fractal past de formule toe op elk punt in het complex vlakte. De kleuren geven aan hoeveel iteraties er nodig zijn voor p(z) om naar (ongeveer) nul te convergeren. De saaie regio's in de fractal zijn de oplossingen van de oorspronkelijke vergelijking.
|
 |
| Meer informatie over Newtonverzamelingen
|
 |
 |
| Newtonverzameling voor p(z) = z3 - 1, a = 0.5 |
 |
| Waar te beginnen
|
| Nu u iets meer over fractals te weten bent gekomen, bent u waarschijnlijk benieuwd hoe u deze met Ultimate Fractal kunt produceren. Utimate Fractal opent standaard met het Mandelbrot fractal. De gemakkelijkste manier om het programma te verkennen is om dit fractal te nemen en te beginnen met inzoomen. Klik en sleep de muiscursor binnen het fractal venster om in te zoomen. Klik de rechter muisknop om uit te zoomen. Ultimate Fractal heeft meer mogelijkheden, maar het is een goed idee om eenvoudig met zoomen te beginnen om een idee te krijgen van wat fractals zijn en hoe Utimate Fractal werkt.
|
 |
 |
 |
 |
 |
| Klik en sleep de muiscursor om in te zoomen. |
|
Het uitvergrote deel van de fractal. |
|
 |
| Fractal Parameters
|
| Het Fractal Parameters venster toont de beeldoorsprong, het maximum aantal iteraties, de vergroting of schaal, de complexe parameter C in de Juliaverzameling en de waarde van de parameter a in de Newtonverzameling. U kunt deze parameters veranderen en op F5 (Vernieuwen) drukken of op de Vernieuwen knop klikken.
|
 |
| X |
De X waarde van de beeldoorsprong. De waarde ligt tussen -2 to 2. |
| Y |
De Y waarde van de beeldoorsprong. De waarde ligt tussen -2 to 2. |
| Iteraties |
Het maximum aantal iteraties (herhalingen) in de berekening van de fractal. De waarde ligt tussen 1 en 10000. Als het maximale aantal iteraties te klein is, wordt de pixel mogelijk verkeerd ingekleurd (zwart). Als het aantal iteraties te groot is kan het erg lang duren voordat de fractal is berekend. |
| Schaal |
De vergroting. Een vergroting van 200 toont de fractal in zijn geheel. |
| X (Julia) |
De X waarde van de complexe parameter C in de Juliaverzameling. |
| Y (Julia) |
De Y waarde van de complexe parameter C in de Juliaverzameling. |
| a (Newton) |
De waarde van de parameter a in de Newtonverzameling. |
|
 |
 |
 |
 |
| Het Fractal Parameters venster toont de beeldoorsprong, het maximum aantal iteraties, de vergroting of schaal, de complexe parameter C in de Juliaverzameling en de waarde van de parameter a in de Newtonverzameling. |
 |
| In en uitzoomen
|
| Klik met de linker muisknop in het fractal venster en versleep de muiscursor om op de getoonde rechthoek in te zoomen. Klik met de rechter muisknop in het fractal venster om uit te zoomen. Om de fractal te herpositioneren klikt u 1 keer op een punt in de fractal zonder de muiscursor te verslepen. Dit punt wordt het nieuwe middelpunt in het fractal venster.
|
 |
 |
Met het commando Inzoomen (F9) kunt u inzoomen op de fractal. |
 |
 |
Met het commando Uitzoomen (F10) kunt u uitzoomen op de fractal. |
|
 |
| Kleuren
|
| De kleur (stijl) bepaalt hoe de fractals worden ingekleurd. De fractal formule genereert de basisvorm van de fractal, de kleurstijl verschaft een manier om deze berekende vorm visueel te maken. Er is grote flexibiliteit om kleuren te combineren, te wijzigen en uit te proberen. Ultimate Fractal maakt het makkelijk om van kleuren en kleurstijl te veranderen. In het Opties menu kunt u uit 4 kleurstijlen kiezen:
|
 |
| Kleurverloop |
De pixels in het fractal worden gekleurd volgens de berekende waarde van de index in een lineair kleurverloop. |
| Kleurverloop 3D |
Kleurverloop met een extra 3D effect. |
| Kleurtoon |
De Kleurtoon component van een pixel wordt aangepast volgens de berekende waarde van de index. |
| Kleurtoon 3D |
Kleurtoon met een extra 3D effect. |
|
 |
 |
Met het commando Random kleuren (F6) kunt u willekeurige kleuren genereren. |
 |
Met het commando Kleurverloop bewerken kunt u een kleurverloop wijzigen. |
 |
Met het commando Open Kleurverloop opent een kleurverloop (geen fractal parameters) uit een eerder opgeslagen parameter bestand (*.fractal). |
|
 |
| Met het Kleurverloop venster kunt u het kleurverloop wijzigen. Verander de kleuren door op één van de kleuren te klikken. Versleep de schuiven om de posities van de tussenliggende kleuren te wijzigen. De posities van de kleuren zijn een percentage van de totale lengte van de lijn waarlangs het kleurverloop gedefinieerd is. Een waarde van 20 geeft aan dat de kleur zich op 20 procent van de totale lengte vanaf het startpunt bevindt. De posities van de kleuren in het control liggen tussen 0 en 100, waarbij de positie van de eerste kleur 0 is en de positie van de laatste kleur 100. Door Kleuren afwisselen te markeren gebruikt u twee afwisselende kleuren.
|
 |
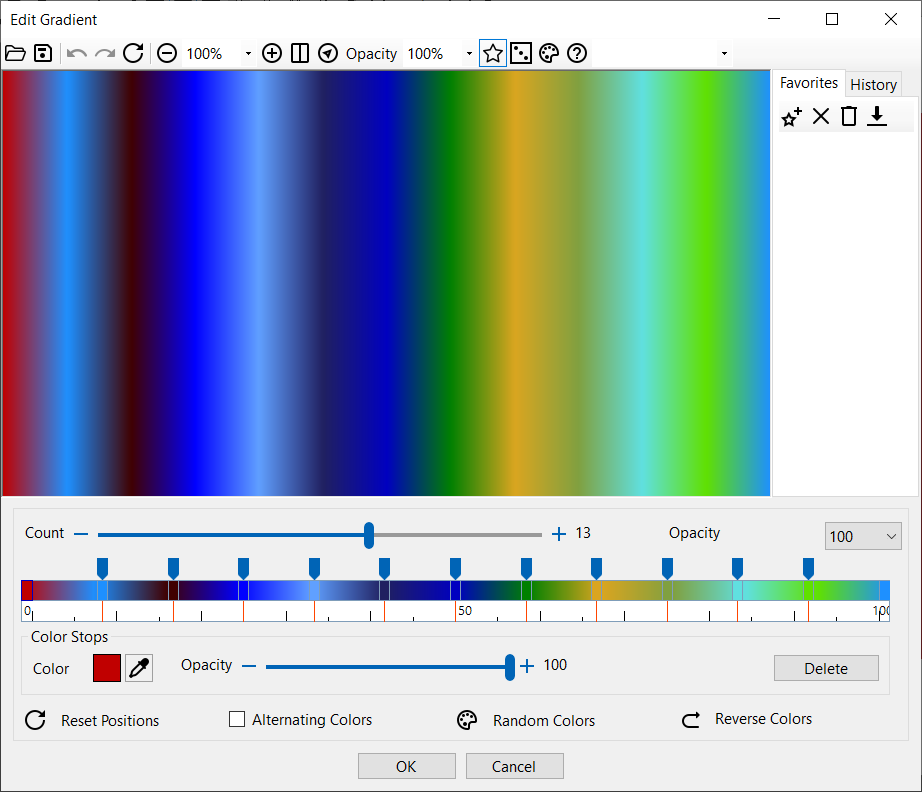 |
| Het Kleurverloop dialoogvenster |
 |
| Als Ultimate Fractal een fractal berekent, berekent het niet direct een kleur voor elke pixel maar een onderliggende index waarde. Het kleurverloop bepaalt aan de hand van deze index waarden de kleuren die de pixels zullen krijgen. Omdat alleen deze index waarden worden opgeslagen, kunnen de kleuren en kleurstijlen gewijzigd worden zonder dat de gehele fractal opnieuw berekend moet worden. Hieronder is een voorbeeld te zien van dezelfde fractal voor 3 verschillende kleurverlopen.
|
 |
|
|
 |
| Het menu Bestand bevat de volgende menu-items:
|
 |
Met het commando Open (Ctrl + O) kunt u een eerder opgeslagen parameter bestand openen (*.fractal). |
 |
Met het commando Parameters opslaan (Ctrl + S) kunt u de fractal parameters opslaan. Een fractal bestand bevat 1 enkele fractal en alle informatie die nodig is om de fractal op te bouwen. De berekende pixels worden niet opgeslagen. Gebruik het commando Afbeelding opslaan om de fractal als afbeelding op te slaan. |
 |
Met het commando Afbeelding opslaan kunt u de fractal als afbeelding opslaan (JPG, PNG, WEBP, GIF, TIF, BMP). |
|
Met het commando Pagina-instelling kunt u pagina details instellen voor het printen in Windows-toepassingen. |
 |
Met het commando Print (Ctrl + P) kunt u de fractal als afbeelding printen. |
|
Met het commando Afdrukvoorbeeld kunt u het voorbeeld bekijken van een af te drukken fractal. |
|
Met het commando Recente bestanden kunt u een fractal uit de lijst met recente bestanden openen. |
|
Met het commando Afsluiten (Ctrl + Q) kunt u het programma afsluiten. |
|
 |
| Het menu Bewerken bevat de volgende menu-items:
|
 |
Met het commando Ongedaan maken (Ctrl + Z) kunt u uw laatste actie ongedaan maken. |
 |
Met het commando Opnieuw uitvoeren (Ctrl + Y) kunt u uw laatste actie opnieuw uitvoeren. |
 |
Met het commando Kopiëren (Ctrl + C) kunt u een afbeelding van de fractal naar het klembord kopiëren. |
 |
Met het commando Terugzetten (Ctrl + R) zet u de Mandelbrot en Julia parameters terug naar de standaardwaarden. |
|
 |
| Het menu Beeld bevat de volgende menu-items:
|
 |
Met het commando Inzoomen (F9) kunt u inzoomen op de fractal. |
 |
Met het commando Uitzoomen (F10) kunt u uitzoomen op de fractal. |
 |
Met het commando Vernieuwen (F5) kunt u de fractal vernieuwen. |
|
 |
| Het menu Opties bevat de volgende menu-items:
|
 |
Met het commando Random kleuren (F6) kunt u willekeurige kleuren genereren. |
|
Met het commando Vooringestelde kleurverlopen kunt u een vooringesteld kleurverloop kiezen. |
 |
Met het commando Kleurverloop bewerken kunt u een kleurverloop wijzigen. |
 |
Met het commando Open Kleurverloop opent een kleurverloop (geen fractal parameters) uit een eerder opgeslagen parameter bestand (*.fractal). |
 |
Met het commando Aan Favorieten toevoegen (Ctrl + F) kunt u fractal parameters (geen kleurinformatie) aan de lijst met Favorieten toevoegen. |
 |
Met het commando Favorieten indelen kunt u fractals verwijderen uit de lijst met Favorieten. |
|
De Favorieten lijst verschaft een eenvoudige manier om veelgebruikte fractal parameters op te slaan, te organiseren en te benaderen. Net als bij een web browser helpt de Favorieten lijst om snel toegang te krijgen tot veel gebruikte items. Met uw fractals in de Favorieten lijst is het niet nodig om op uw computer naar bestanden te zoeken. Als u een favoriet opent worden alleen de fractal parameters geladen, geen kleurinformatie. Gebruik het Open commando om fractal parameters met kleurinformatie te openen. De Favorieten folder kunt u vinden in de directory van de toepassing (C:\Program Files\Pop Art Studio\Fractals). |
|
 |
| Het menu Help bevat de volgende menu-items:
|
 |
Met het commando Help (F1) kunt u de help opstarten. |
 |
Met het commando Taal kunt u de taal wijzigen. |
|
Met het commando Bestellen kunt u het programma online bestellen. |
 |
Met het commando Registratiecode invoeren kunt u uw registratiecode invoeren. |
 |
Met het commando Over Ultimate Fractal kunt u de versie en het versie overzicht, de website en het contact email adres tonen. |
|
 |
| Voor opmerkingen, vragen en suggesties kunt u een email sturen naar: contact@fotoview.nl.
|