| Ultimate Fractal
|
 |
| Über Fraktale |
| Die Mandelbrot-Menge |
| Julia-Mengen |
| Newton-Mengen |
| Wo soll ich anfangen |
| Fraktalparameter |
| Ein- und Auszoomen |
| Farben |
| Das Datei-Menü |
| Das Bearbeiten-Menü |
| Das Ansicht-Menü |
| Das Optionen-Menü |
| Das Hilfe-Menü |
 |
|
Über Fraktale
|
| Ein Fraktal ist in der Regel eine ungleichmäßige oder fragmentierte geometrische Form, die so aufsplittet werden kann, dass nahezu alle Komponenten eine kleinere Kopie des Ganzen sind. Diese Eigenschaft wird als Selbstähnlichkeit bezeichnet. Der Begriff 'Fraktal' wurde von Benoît Mandelbrot im Jahr 1975 eingeprägt und leitet sich vom lateinischen Wort 'fractus' her, welches 'gebrochen' oder 'in Stücke zerbrochen' bedeutet. Da Fraktale bei allen Vergrößerungsstufen ähnlich aussehen, werden sie oft als unendlich komplexe Strukturen betrachtet. Fraktale Konzepte findet man auch in der Natur, wobei die Anzahl der Stufen von selbstähnlichen Strukturen jedoch begrenzt ist. Hierzu zählen Wolken, Bergketten, Blitzschläge, Küstenlinien und Schneeflocken. |
 |
| Mehr Informationen über Fraktale
|
 |
 |
 |
 |
 |
| Die Mandelbrot-Menge ist ein berühmtes Beispiel eines Fraktals. |
|
Ein näherer Blick auf die Mandelbrot-Menge. |
|
 |
| Die Mandelbrot-Menge
|
| Die im Jahr 1980 von Benoît Mandelbrot entdeckte Mandelbrot-Menge ist wahrscheinlich das bekannteste Fraktal. Ähnlich wie Julia-Mengen wird es trotz seiner unglaublichen Komplexität durch eine sehr einfache Formel generiert. Die Mandelbrot-Menge ist nicht exakt selbstähnlich, denn obwohl Teilstrukturen des originalen Fraktals beim Heranzoomen wieder erscheinen, sind sie oft deformiert und zeigen andere Ornamente. Das ist auch der Grund, warum das Hineinzoomen in dieses Fraktal so interessant ist: man weiß nie, was man als Nächstes sehen wird. Die Mandelbrot-Menge wird durch die folgende Formel erzeugt: zn+1 = zn2 + c wobei z und c komplexe Zahlen: z = x + iy, z0 = 0, und c ein Punkt der komplexen Zahlenebene sind. Die Formel iteriert so lange, bis |zn| (der Betrag von z) größer oder gleich dem sog. Bailout-Wert 2 ist. Dann wird das Pixel, für das c steht, gemäß der Anzahl von Iterationen eingefärbt, die durchlaufen werden, bis der Prozess den Grenzwert überschritten hat. Der uninteressante schwarze Bereich im Bild ist die eigentliche Mandelbrot-Menge. Er besteht aus sämtlichen Werten für c, für die gilt, dass |zn| nie größer als 2 geworden ist. Selbstverständlich ist es unmöglich, diesen Bereich exakt zu berechnen. Aus diesem Grund färbt das Programm alle Pixel schwarz ein, für die |zn| nie größer als 2 für eine gegebene Anzahl von Iterationen wird, zum Beispiel 256. Die Kubische Mandelbrot-Menge wird durch die folgende Formel erzeugt: zn+1 = zn3 + c Die Quadratische Mandelbrot-Menge wird durch die folgende Formel erzeugt: zn+1 = zn4 + c
|
 |
| Mehr Informationen über die Mandelbrot-Menge
|
 |
 |
 |
 |
 |
| Die Kubische Mandelbrot-Menge |
|
Die Quadratische Mandelbrot-Menge |
|
 |
| Julia-Mengen
|
| Einen der bekanntesten und wichtigsten Fraktaltypen stellt die Familie von Julia-Mengen dar, welche vom französischen Mathematiker Gaston Julia während des Ersten Weltkrieges entdeckt wurde. Julia-Mengen werden durch eine einfache Formel mit einem komplexen Parameter namens C oder Samen generiert. Dieser Parameter kann variiert werden und ist ausschlaggebend dafür, was für eine Form die fraktale Struktur annimmt. Julia-Mengen sind ebenfalls selbstähnlich.
|
 |
| Mehr Informationen über Julia-Mengen
|
 |
 |
| Julia-Menge für C = [0,4, 0,6] |
 |
| Newton-Mengen
|
| Dieses Fraktal wird erzeugt, indem versucht wird, die Gleichung z3 = 1 unter Verwendung der Newton-Raphson-Methode zu lösen, wobei z eine komplexe Zahl ist: z = x + iy. Das zieht eine Definition der Funktion p(z) = z3 - 1 nach sich, die ihrerseits in einer iterativen Formel verwendet wird, die gegen Null konvergieren soll. Demzufolge muss ein Wert für z gefunden werden, welcher eine Lösung der ersten Gleichung ist. Eine Verallgemeinerung von Newton-Iteration ist:zn+1 = zn - a * p(zn) / p'(zn) Wobei a eine beliebige komplexe Zahl und p'(z) die Ableitung von p(z) sind. Eine spezielle Auswahl von a = 1 bezieht sich auf das Newton-Fraktal. Dieses Fraktal wendet die Formel für jeden Punkt der komplexen Zahlebene an und färbt ihn gemäß der Anzahl von Iterationen ein, die erforderlich sind, damit p(z) (annähernd) gegen Null konvergiert. Die langweiligen Bereiche des Fraktals stellen die eigentlichen Lösungen der Originalgleichung dar.
|
 |
| Mehr Informationen über Newton-Mengen
|
 |
 |
| Newton-Menge für p(z) = z3 - 1, a = 0.5 |
 |
| Wo soll ich anfangen
|
| Da Sie nun ein bisschen mehr über Fraktale wissen, möchten Sie wahrscheinlich erfahren, wie man sie unter Verwendung von Ultimate Fractal erzeugen kann. Standardmäßig öffnet das Programm mit einer Mandelbrot-Menge, einem gängigen Fraktaltyp. Der einfachste Weg besteht also darin, dass man sich dieses Fraktal vornimmt und beginnt, es zu zoomen. Hierzu klicken und ziehen Sie innerhalb des Fraktal-Fensters, um einen Fraktalausschnitt zu vergrößern. Wenn Sie wieder herauszoomen möchten, klicken Sie einfach mit der rechten Maustaste. Ultimate Fractal verfügt über viel mehr Möglichkeiten, aber es ist empfehlenswert, zunächst mit einem einfach Zoomen anzufangen, um ein Gefühl sowohl für Fraktale als auch für die Arbeit mit dem Programm aufzubauen.
|
 |
 |
 |
 |
 |
| Klicken und ziehen Sie innerhalb des Fraktal-Fensters, um einen Fraktalausschnitt zu vergrößern. |
|
Der vergrößerte Teil des Fraktals. |
|
 |
| Fraktalparameter
|
| Das Fenster mit Fraktalparametern zeigt die Koordinaten des Mittelpunktes eines Ausschnittes, für den das Fraktal berechnet werden soll, die maximale Anzahl von Iterationen, den Vergrößerungs- oder Skalierungsgrad, den komplexen Parameter C, der bei Julia-Mengen verwendet wird sowie den Wert des Parameters a, der bei Newton-Mengen verwendet wird. Sie können diese Parameter ändern, indem Sie Ihre eigenen Werte eingeben und anschließend durch Tätigen der F5-Taste (Aktualisieren) oder Anklicken der Taste 'Aktualisieren' übernehmen lassen.
|
 |
| X |
Der X-Wert des Mittelpunktes eines Ausschnittes, für den das Fraktal berechnet werden soll. Diese Einstellung kann im Bereich von -2 bis 2 vorgenommen werden. |
| Y |
Der Y-Wert des Mittelpunktes eines Ausschnittes, für den das Fraktal berechnet werden soll. Diese Einstellung kann im Bereich von -2 bis 2 vorgenommen werden. |
| Iterationen |
Die maximale Anzahl von Iterationen bei der Berechnung des Fraktals. Der Parameter kann Werte aus dem Bereich 1 bis 10000 annehmen. Ist die maximale Berechnungstiefe zu klein eingestellt, werden die Pixel inkorrekt eingefärbt (schwarz). Andererseits müssen viele Iterationen durchgeführt werden, wenn die Anzahl der Durchläufe zu hoch ist, was zu einer langsamen Fraktalberechnung führen kann. |
| Skalierung |
Die Vergrößerung. Bei einer 200-fachen Vergrößerung wird das ganze Fraktal angezeigt. |
| X (Julia) |
Der X-Wert des komplexen Parameters C, der bei Julia-Mengen verwendet wird. |
| Y (Julia) |
Der Y-Wert des komplexen Parameters C, der bei Julia-Mengen verwendet wird. |
| a (Newton) |
Der Wert des Parameters a, der bei Newton-Mengen verwendet wird. |
|
 |
 |
 |
 |
| Das Fenster mit Fraktalparametern zeigt die Koordinaten des Mittelpunktes eines Ausschnittes, für den das Fraktal berechnet werden soll, die maximale Anzahl von Iterationen, den Vergrößerungs- oder Skalierungsgrad, den komplexen Parameter C, der bei Julia-Mengen verwendet wird sowie den Wert des Parameters a, der bei Newton-Mengen verwendet wird. |
 |
| Ein- und Auszoomen
|
| Um näher heranzuzoomen, klicken Sie mit der linken Maustaste und halten Sie sie gedrückt, wenn Sie den Cursor innerhalb des Fraktal-Fensters ziehen. Zum Herauszoomen klicken Sie mit der rechten Maustaste. Wenn Sie das Fraktal neu positionieren wollen, klicken Sie einen Punkt im Fraktal mit der linken Maustaste an. Dieser Punkt wird zum neuen Mittelpunkt im Fraktal-Fenster.
|
 |
 |
Der Befehl Einzoomen (F9) gibt Ihnen die Möglichkeit, die Ansicht auf das Fraktal zu vergrößern. |
 |
 |
Der Befehl Auszoomen (F10) gibt Ihnen die Möglichkeit, die Ansicht auf das Fraktal zu verkleinern. |
|
 |
| Farben
|
| Ein Farbmodus legt fest, wie Fraktale farblich dargestellt werden sollen. Die Fraktalformel erzeugt die Grundform des Fraktals, während der Farbmodus bestimmt, wie diese Form eingefärbt werden soll. Dies gibt Ihnen die Flexibilität, Farbmodi mit jedem Fraktal frei zu kombinieren. Ultimate Fractal macht es einfach, zwischen Farbmodi zu wechseln. Wählen Sie einfach einen von vier verfügbaren Einstellungen aus dem Menü 'Optionen':
|
 |
| Farbverlauf |
Die Pixel werden gemäß des berechneten Indexwertes in einem linearen Farbverlauf eingefärbt. |
| Farbverlauf 3D |
Ein 3D-Effekt, der dem Modus 'Farbverlauf' hinzugefügt wird. |
| Abweichung vom Farbton |
Die Farbton-Komponente vom Pixel wird gemäß des berechneten Indexwertes geändert. |
| Abweichung vom Farbton 3D |
Ein 3D-Effekt, der dem Modus 'Abweichung vom Farbton' hinzugefügt wird. |
|
 |
 |
Der Befehl Zufällige Farben (F6) gibt Ihnen die Möglichkeit, zufällige Farben zu generieren. |
 |
Der Befehl Farbverlauf bearbeiten gibt Ihnen die Möglichkeit, den Farbverlauf zu ändern. |
 |
Der Befehl Farbverlauf öffnen gibt Ihnen die Möglichkeit, einen Farbverlauf (keine anderen Parameter) aus einer zuvor gespeicherten Parameterdatei (*.fractal) zu öffnen. |
|
 |
| Das Dialogfenster Farbverlauf gibt Ihnen die Möglichkeit, den Farbverlauf zu modifizieren. Sie können die Farben ändern, indem Sie eine von ihnen anklicken. Verschieben Sie den Positionsreiter, um die Positionen der Interpolationsfarben zu verändern. Die Farbpositionen im Verlaufsbedienfeld legen einen Prozentanteil der Entfernung entlang der Farbverlauflinie fest. Zum Beispiel gibt ein Wert von 20 an, dass die gewählte Farbe genau nach 20% der Gesamtstrecke vom Startpunkt erscheint. Die Positionen in diesem Kontrollfenster repräsentieren folglich Werte aus dem Bereich von 0 bis 100. Dabei muss sich die erste Farbe im Farbverlauf auf der Position 0 und die letzte auf der Position 100 befinden. Wenn zwei alternierende Farben verwendet werden sollen, wählen Sie die Option 'Alternierende Farben' aus.
|
 |
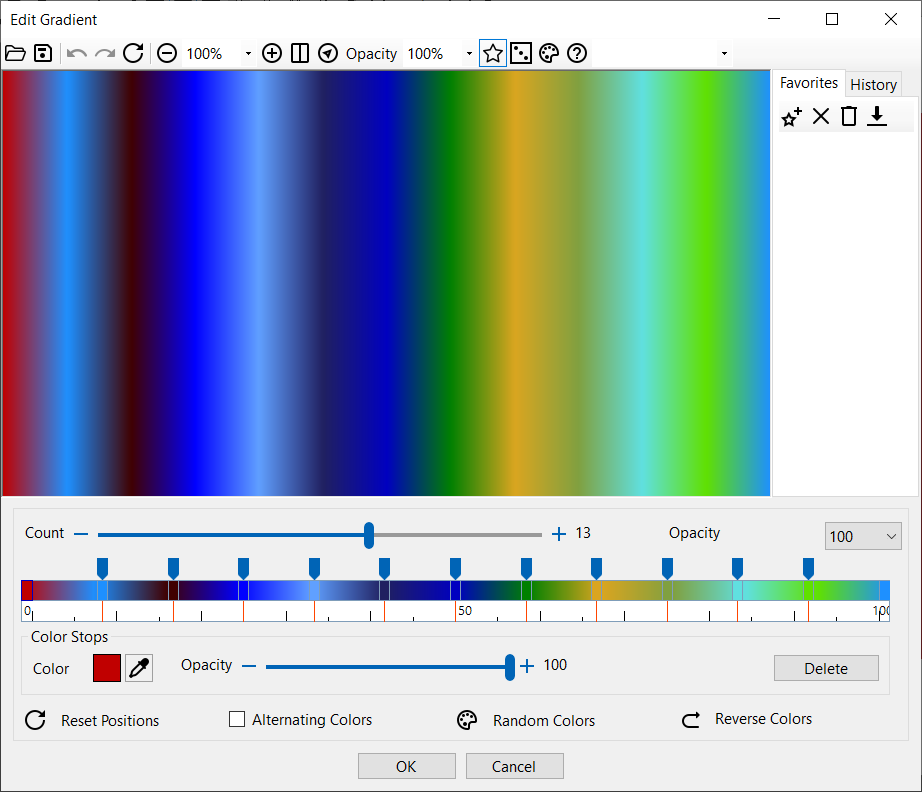 |
| Das Dialogfenster Farbverlauf |
 |
| Wenn Ultimate Fractal ein Fraktal berechnet, ermittelt es nicht sofort eine Farbe für jedes Pixel. Stattdessen wird ein intermediärer Indexwert errechnet. Ein Farbverlauf übersetzt Indexwerte in Farben. Da nur Indexwerte gespeichert werden, können die Farben sowie die Farbmodi geändert werden, ohne dass das Fraktal neu kalkuliert werden muss. Hier ist ein Beispiel eines Fraktals mit drei verschiedenen Farbverläufen.
|
 |
|
|
 |
| Das Menü Datei enthält folgende Menüpunkte:
|
 |
Der Befehl Öffnen (Strg + O) öffnet eine vorher gespeicherte Datei (*.fractal). |
 |
Der Befehl Parameter speichern (Strg + S) speichert die Fraktalparameter. Eine Fraktal-Datei enthält ein einzelnes Fraktal samt aller Informationen, die zur seiner Wiederherstellung benötigt werden. Die berechneten Pixel werden nicht abgespeichert. Verwenden Sie den Befehl Als Bild speichern, wenn Sie das Fraktal in Form eines Bildes speichern wollen. |
 |
Der Befehl Als Bild speichern speichert das Fraktal in einem Bildformat (JPG, PNG, WEBP, GIF, TIF, BMP). |
|
Der Befehl Seite einrichten gibt Ihnen die Möglichkeit, die Seiteneigenschaften für das Drucken in Windows-Anwendungen festzulegen. |
 |
Der Befehl Drucken (Strg + P) gibt Ihnen die Möglichkeit, das Fraktal zu drucken. |
|
Der Befehl Druckvorschau gibt Ihnen die Möglichkeit, einen Vorabblick auf das Aussehen des auszudruckenden Fraktals zu werfen. |
|
Der Befehl Letzte Dateien gibt Ihnen die Möglichkeit, ein Fraktal von der Liste mit den zuletzt verwendeten Dateien zu öffnen. |
|
Der Befehl Beenden (Strg + Q) gibt Ihnen die Möglichkeit, das Programm zu schließen. |
|
 |
| Das Menü Bearbeiten enthält folgende Menüpunkte:
|
 |
Der Befehl Rückgängig (Strg + Z) gibt Ihnen die Möglichkeit, Ihren letzten Vorgang rückgängig zu machen. |
 |
Der Befehl Wiederherstellen (Strg + Y) gibt Ihnen die Möglichkeit, Ihren letzten rückgängig gemachten Vorgang wiederherzustellen. |
 |
Der Befehl Kopieren (Strg + C) gibt Ihnen die Möglichkeit, ein Fraktalbild in den Zwischenspeicher abzulegen. |
 |
Der Befehl Zurücksetzen (Strg + R) gibt Ihnen die Möglichkeit, die Standardwerte für die Mandelbrot- und Julia-Parameter wiederherzustellen. |
|
 |
| Das Menü Ansicht enthält folgende Menüpunkte:
|
 |
Der Befehl Einzoomen (F9) gibt Ihnen die Möglichkeit, die Ansicht auf das Fraktal zu vergrößern. |
 |
Der Befehl Auszoomen (F10) gibt Ihnen die Möglichkeit, die Ansicht auf das Fraktal zu verkleinern. |
 |
Der Befehl Aktualisieren (F5) gibt Ihnen die Möglichkeit, das Fraktal zu aktualisieren. |
|
 |
| Das Menü Optionen enthält folgende Menüpunkte:
|
 |
Der Befehl Zufällige Farben (F6) gibt Ihnen die Möglichkeit, zufällige Farben zu generieren. |
|
Der Befehl Vordefinierte Farbverläufe gibt Ihnen die Möglichkeit, einen vordefinierten Farbverlauf auszuwählen. |
 |
Der Befehl Farbverlauf bearbeiten gibt Ihnen die Möglichkeit, den Farbverlauf zu ändern. |
 |
Der Befehl Farbverlauf öffnen gibt Ihnen die Möglichkeit, einen Farbverlauf (keine anderen Parameter) aus einer zuvor gespeicherten Parameterdatei (*.fractal) zu öffnen. |
 |
Der Befehl Zu Favoriten hinzufügen (Strg + F) gibt Ihnen die Möglichkeit, die Fraktalparameter (ohne den Farbmodus und die Farben des Farbverlaufs) zu Ihrer Favoritenliste hinzuzufügen. |
 |
Der Befehl Favoriten organisieren gibt Ihnen die Möglichkeit, Fraktale aus Ihrer Favoritenliste zu entfernen. |
|
Die Favoritenliste gibt Ihnen eine bequeme Möglichkeit, auf häufig verwendete Fraktalparameter zuzugreifen und sie zu organisieren. Ähnlich wie Lesezeichen in einem Webbrowser hilft Ihnen die Favoritenliste dabei, auf oft benutzte Einstellungen schnell zuzugreifen. Wenn Sie Ihre Fraktale auf der Favoritenliste haben, können Sie sie schnell öffnen, ohne nach den richtigen Dateien suchen zu müssen. Wählen Sie eine der Positionen aus der Liste, werden ausschließlich die Fraktalparameter und keine Farbinformationen geladen. Verwenden Sie den Befehl Datei öffnen, um ein Fraktal samt seiner Farbinformationen zu öffnen. Der Ordner Favoriten befindet sich im Anwendungsverzeichnis (C:\Program Files\Pop Art Studio\Fractals). |
|
 |
| Das Menü Hilfe enthält folgende Menüpunkte:
|
 |
Der Befehl Hilfe (F1) gibt Ihnen die Möglichkeit, die Hilfeseite anzuzeigen. |
 |
Der Befehl Sprache gibt Ihnen die Möglichkeit, die Sprache für das Programm zu ändern. |
|
Der Befehl Bestellen gibt Ihnen die Möglichkeit, das Programm online zu bestellen. |
 |
Der Befehl Lizenzschlüssel eingeben gibt Ihnen die Möglichkeit, das Programm durch die Eingabe Ihres Registrierungsschlüssels freizuschalten. |
 |
Der Befehl Über Ultimate Fractal gibt Ihnen die Möglichkeit, sich über die aktuelle Programmversion, den Versionsverlauf, die Website und die Kontakt-E-Mail-Adresse zu informieren. |
|
 |
| Wenn Sie irgendwelche Bemerkungen, Fragen oder Vorschläge haben, schicken Sie uns bitte eine E-Mail an:: contact@fotoview.nl.
|
|


































