| Ultimate Fractal
|
 |
| À propos des Fractales |
| L'ensemble de Mandelbrot |
| L'ensemble de Julia |
| L'ensemble de Newton |
| Où commencer |
| Paramètres de la fractale |
| Zoom avant et arrière |
| Couleurs |
| Le menu Fichier |
| Le menu Édition |
| Le menu Affichage |
| Le menu Options |
| Le menu Aide |
 |
|
À propos des Fractales
|
| Une fractale est une figure géométrique irrégulière à toutes les échelles. Les fractales possèdent une quantité infinie de détails et, pour certaines d'entre elles, des motifs se répètent à des échelles toujours plus réduites. En générale, les fractales peuvent être générées par l'application répétée d'une modification spécifique (mathématique). Le terme fractale a été introduit en 1975 par Benoît Mandelbrot et est dérivé du latin fractus (cassé). |
 |
| En savoir plus sur les fractales
|
 |
 |
 |
 |
 |
| L'ensemble de Mandelbrot est un exemple connu de fractale. |
|
Observer de plus près l'ensemble de Mandelbrot. |
|
 |
| L'ensemble de Mandelbrot
|
| L'ensemble de Mandelbrot est une fractale qui joue un rôle important dans la théorie du chaos. L'ensemble a été nommé d'après Benoît Mandelbrot, mathématicien polono-français qui, pour la première fois, en 1980, a étudié la fractale à l'aide d'un ordinateur. En dehors de la théorie du chaos, l'ensemble de Mandelbrot est surtout connu pour ses caractéristiques esthétiques. Cela vaut vraiment la peine de zoomer avant sur l'ensemble, on ne sait jamais sur quoi on va tomber. L'ensemble de Mandelbrot est généré par la formule : zn+1 = zn2 + c où z et c sont des valeurs complexes : z = x + iy, z0 = 0 et c est un point dans la surface complexe. La formule est terminée lorsque |zn| (la longueur de z) est plus grande que ou égale à la valeur d'échappement de 2. Le pixel en rapport avec c devient dépendant du nombre d'itérations qui se sont précédemment colorées. Les zones noires inintéressantes de l'image forment en fait l'ensemble de Mandelbrot. Elles se composent de toutes les valeurs de c pour lesquelles |zn| ne dépasse jamais 2. Il est naturellement impossible de calculer précisément cette zone, c'est pourquoi le programme associe le noir à tous les pixels pour lesquels |zn| ne dépasse jamais 2 pour un nombre maximum donné d'itérations, par exemple 256. L'ensemble cubique de Mandelbrot est généré par la formule : zn+1 = zn3 + c L'ensemble quadratique de Mandelbrot est généré par la formule : zn+1 = zn4 + c
|
 |
| En savoir plus sur l'ensemble de Mandelbrot
|
 |
 |
 |
 |
 |
| L'ensemble cubique de Mandelbrot |
|
L'ensemble quadratique de Mandelbrot |
|
 |
| L'ensemble de Julia
|
| L'un des types les plus basiques de fractales est la famille des ensembles de Julia, découverts pendant la première guerre mondiale par le mathématicien français Gaston Julia. Les ensembles de Julia sont calculés selon une formule simple avec un paramètre C complexe. En faisant varier ce paramètre, il est possible de générer un grand nombre de fractales différentes. Les ensembles de Julia permettent également de faire se reproduire des motifs à des échelles toujours plus réduites.
|
 |
| En savoir plus sur les ensembles de Julia
|
 |
 |
| L'ensemble de Julia pour C = [-0.4, 0.6]. |
 |
| L'ensemble de Newton
|
| Cette fractale est créée par la résolution de la comparaison z3 = 1 à l'aide de la méthode Newton-Raphson, selon laquelle z est une valeur complexe : z = x + iy. En définissant la fonction p(z) = z3 - 1 et en utilisant celle-ci dans une formule itérative qui doit converger vers zéro, on obtient une valeur de z comme résolution de la comparaison. Une formule générale pour l'itération de Newton est :zn+1 = zn - a * p(zn) / p'(zn) où a est une valeur complexe et p'(z) la dérivée de p(z). La valeur spéciale a = 1 est conforme à la fractale de Newton. La fractale adapte la formule à chaque point de la surface complexe. Les couleurs indiquent combien d'itérations sont nécessaires pour faire converger p(z) vers (environ) zéro. Les zones ennuyeuses de la fractale sont les résolutions de la comparaison d'origine.
|
 |
| En savoir plus sur l'ensemble de Newton
|
 |
 |
| L'ensemble de Newton pour p(z) = z3 - 1, a = 0.5 |
 |
| Où commencer
|
| À présent que vous en savez davantage sur les fractales, vous vous demandez certainement comment les produire à l'aide de l'outil Ultimate Fractal. Utimate Fractal s'ouvre par défaut avec la fractale de Mandelbrot. La manière la plus simple de découvrir ce programme est de prendre cette fractale et de commencer par effectuer un zoom avant. Cliquez et faites glisser le pointeur dans la fenêtre de la fractale pour zoomer avant. Cliquez droit pour effectuer un zoom arrière. Ultimate Fractal offre davantage de possibilités, mais il est bon de commencer par quelque chose de facile en utilisant le zoom, afin de se faire une bonne idée de ce que sont les fractales et de la manière dont Ultimate Fractal fonctionne.
|
 |
 |
 |
 |
 |
| Cliquez et faites glisser le pointeur pour zoomer avant. |
|
La partie agrandie de la fractale. |
|
 |
| Paramètres de la fractale
|
| La fenêtre Paramètres de la fractale affiche l'origine de l'image, le nombre maximum d'itérations, l'agrandissement ou l'échelle, le paramètre complexe C utilisé dans l'ensemble de Julia et la valeur du paramètre a utilisé dans l'ensemble de Newton. Vous pouvez modifier ces paramètres et appuyer sur F5 (Actualiser) ou cliquer sur le bouton Actualiser.
|
 |
| X |
La valeur X de l'origine de l'image. La valeur est entre -2 et 2. |
| Y |
La valeur Y de l'origine de l'image. La valeur est entre -2 et 2. |
| Itérations |
Le nombre maximum d'itérations (répétitions) dans le calcul de la fractale. La valeur est entre 1 et 10 000. Si le nombre maximum d'itérations est trop faible, il se peut que le pixel prenne la mauvaise teinte et devienne noir. Si le nombre d'itérations est trop élevé, le calcul de la fractale peut prendre énormément de temps. |
| Échelle |
L'agrandissement. Un agrandissement de 200 affiche la totalité de la fractale. |
| X (Julia) |
La valeur X du paramètre complexe C dans l'ensemble de Julia. |
| Y (Julia) |
La valeur Y du paramètre complexe C dans l'ensemble de Julia. |
| a (Newton) |
La valeur du paramètre a dans l'ensemble de Newton. |
|
 |
 |
 |
 |
| La fenêtre Paramètres de la fractale affiche l'origine de l'image, le nombre maximum d'itérations, l'agrandissement ou l'échelle, le paramètre complexe C utilisé dans l'ensemble de Julia et la valeur du paramètre a utilisé dans l'ensemble de Newton. |
 |
| Zoom avant et arrière
|
| Cliquez gauche dans la fenêtre de la fractale et faites glisser le pointeur pour effectuer un zoom avant sur le rectangle affiché. Cliquez droit dans la fenêtre de la fractale pour effectuer un zoom arrière. Pour repositionner la fractale, cliquez une fois sur un point de la fractale, sans faire glisser le pointeur. Ce point devient le nouveau centre dans la fenêtre de la fractale.
|
 |
 |
La commande Zoom avant (F9) vous permet d'effectuer un zoom avant sur la fractale. |
 |
 |
La commande Zoom arrière (F10) vous permet d'effectuer un zoom arrière sur la fractale. |
|
 |
| Couleurs
|
| La couleur (style) définit la manière dont les fractales sont colorées. La formule de la fractale génère la forme de base de la fractale, le style de couleur permet de visualiser cette forme calculée. Cet outil offre une grande flexibilité pour combiner les couleurs et effectuer des modification ou des essais. Ultimate Fractal simplifie les changements de couleurs et de style de couleurs. Vous pouvez choisir parmi 4 styles de couleurs dans le menu Options :
|
 |
| Dégradé |
Les pixels de la fractale sont colorés en fonction de la valeur calculée de l'index dans un dégradé linéaire. |
| Dégradé 3D |
Dégradé avec effet 3D supplémentaire. |
| Teinte |
Le composant de Teinte d'un pixel est adapté en fonction de la valeur calculée de l'index. |
| Teinte 3D |
Teinte avec effet 3D supplémentaire. |
|
 |
 |
La commande Couleurs aléatoires (F6) vous permet de générer des couleurs de manière aléatoire. |
 |
La commande Modifier Dégradé vous permet de modifier un dégradé. |
 |
La commande Ouvrir dégradé vous permet d'ouvrir un dégradé (sans paramètres de fractale) à partir d'un fichier de paramètres précédemment enregistré (*.fractal). |
|
 |
| La fenêtre Dégradé vous permet de modifier le dégradé. Modifiez les couleurs en cliquant sur l'une des couleurs. Faites glisser les cases de défilement pour déplacer les couleurs d'interpolation. Les positions des couleurs sont un pourcentage de la longueur totale de la ligne le long de laquelle le dégradé est défini. Une valeur de 20 permet de spécifier que la couleur est à 20 % de la longueur totale à partir du point de départ. Les couleurs dans cette commande sont positionnées selon des valeurs entre 0 et 100, selon lesquelles la position de la première couleur est 0 et la position de la dernière couleur est 100. L'utilisation de l'outil Alternance des couleurs vous permet d'alterner entre deux couleurs.
|
 |
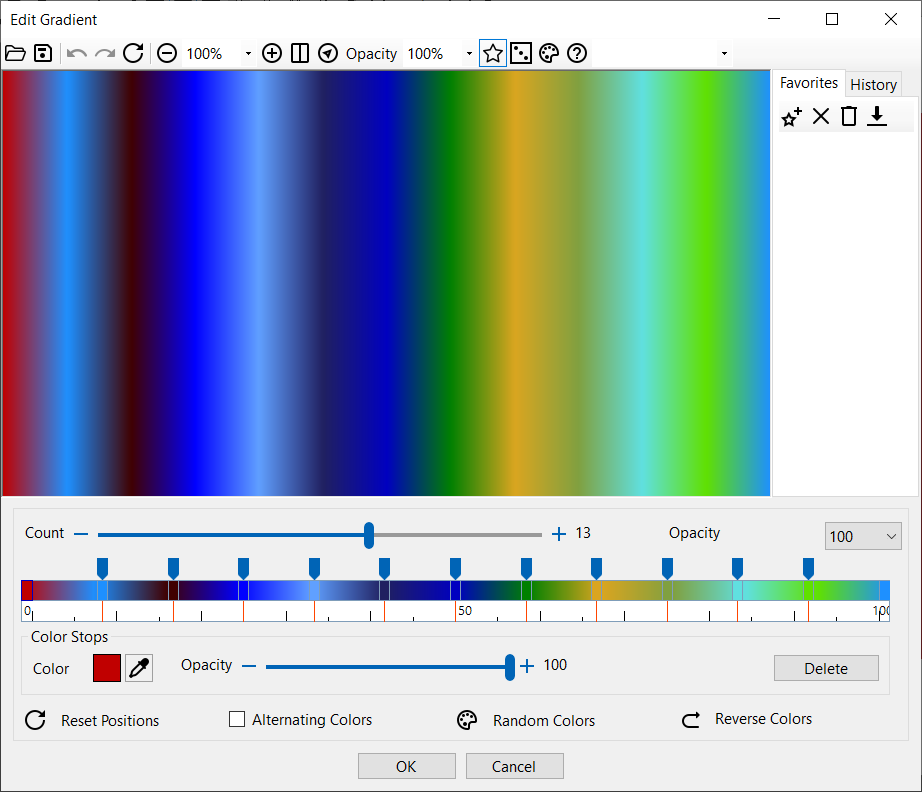 |
| La fenêtre Dégradé. |
 |
| Lorsque Ultimate Fractal calcule une fractale, il ne calcule pas directement une couleur pour chaque pixel, mais une valeur d'index sous-jacente. Le dégradé définit les couleurs qui seront attribuées aux pixels selon ces valeurs d'index. Étant donné que seules ces valeurs d'index sont enregistrées, les couleurs et styles de couleurs peuvent être modifiés sans que la totalité de la fractale doive être recalculée. Vous trouverez ci-dessous un exemple de la même fractale pour 3 dégradés différents.
|
 |
|
|
 |
| Le menu Fichier contient les éléments de menu suivants :
|
 |
La commande Ouvrir (Ctrl + O) vous permet d'ouvrir un fichier de paramètres précédemment sauvegardé (*.fractal). |
 |
La commande Enregistrer paramètres (Ctrl + S) vous permet d'enregistrer les paramètres de la fractale. Un fichier de fractale contient une seule fractale et toutes les informations nécessaires pour la construire. Les pixels calculés ne sont pas enregistrés. Utilisez la commande Enregistrer image pour sauvegarder la fractale en tant qu'image. |
 |
La commande Enregistrer image vous permet de sauvegarder la fractale en tant qu'image (JPG, PNG, WEBP, GIF, TIF, BMP). |
|
La commande Mise en page vous permet d'établir les détails d'une page pour l'imprimer sous une application Windows. |
 |
La commande Imprimer (Ctrl + P) vous permet d'imprimer la fractale en tant qu'image. |
|
La commande Aperçu avant impression vous permet de visionner l'aperçu d'une fractale que vous souhaitez imprimer. |
|
La commande Fichiers récents vous permet d'ouvrir une fractale à partir de la liste contenant des fichiers récents. |
|
La commande Quitter (Ctrl + Q) vous permet de quitter le programme. |
|
 |
| Le menu Édition contient les éléments de menu suivants :
|
 |
La commande Annuler (Ctrl + Z) vous permet d'annuler votre dernière opération. |
 |
La commande Refaire (Ctrl + Y) vous permet de refaire votre dernière opération. |
 |
La commande Copier (Ctrl + C) vous permet de copier une image de la fractale vers le presse-papiers. |
 |
La commande Restaurer (Ctrl + R) vous permet de restaurer les paramètres Mandelbrot et Julia aux valeurs par défaut. |
|
 |
| Le menu Affichage contient les éléments de menu suivants :
|
 |
La commande Zoom avant (F9) vous permet d'effectuer un zoom avant sur la fractale. |
 |
La commande Zoom arrière (F10) vous permet d'effectuer un zoom arrière sur la fractale. |
 |
La commande Actualiser (F5) vous permet de rafraîchir la fractale. |
|
 |
| Le menu Options contient les éléments de menu suivants :
|
 |
La commande Couleurs aléatoires (F6) vous permet de générer des couleurs de manière aléatoire. |
|
La commande Dégradé prédéfinis vous permet de choisir un dégradé précédemment enregistré. |
 |
La commande Modifier Dégradé vous permet de modifier un dégradé. |
 |
La commande Ouvrir dégradé vous permet d'ouvrir un dégradé (sans paramètres de fractale) à partir d'un fichier de paramètres précédemment enregistré (*.fractal). |
 |
La commande Ajouter aux favoris (Ctrl + F) vous permet d'ajouter des paramètres de fractale (sans informations de couleurs) à la liste de Favoris. |
 |
La commande Organiser les favoris vous permet de supprimer des fractales de la liste de Favoris. |
|
La Liste de favoris permet d'enregistrer facilement les paramètres de fractale fréquemment utilisés, de les organiser et d'y accéder. De la même manière qu'un navigateur web, la Liste de favoris vous permet d'accéder rapidement aux éléments fréquemment utilisés. En plaçant vos fractales dans la Liste de favoris vous n'avez plus besoin de rechercher ces fichiers dans votre ordinateur. Lorsque vous ouvrez un fichier de favoris, seuls les paramètres de fractale se chargent, sans informations de couleurs. Utilisez la commande Ouvrir pour ouvrir les paramètres de fractale avec des informations de couleurs. Le Dossier de favoris se trouve dans le dossier d'application (C:\Programmes\Pop Art Studio\Fractals). |
|
 |
| Le menu Aide contient les éléments de menu suivants :
|
 |
La commande Aide (F1) vous permet de lancer l'aide. |
 |
La commande Langue vous permet de changer de langue. |
|
La commande Commander vous permet de commander le programme en ligne. |
 |
La commande Entrer la clé d'enregistrement vous permet de saisir le code d'enregistrement. |
 |
La commande À propos de Ultimate Fractal vous permet d'afficher la version et l'aperçu de version, le site internet et l'adresse e-mail de contact. |
|
 |
| Pour toutes remarques, questions ou suggestions, envoyez un e-mail à: contact@fotoview.nl.
|