| Ultimate Fractal
|
 |
| Sobre las Fractales |
| Conjunto de Mandelbrot |
| Conjuntos de Julia |
| Conjuntos de Newton |
| Dónde empezar |
| Parámetros de una Fractal |
| Aumentar y reducir la imagen |
| Colores |
| El menú Archivo |
| El menú Editar |
| El menú Vista |
| El menú Opciones |
| El menú Ayuda |
 |
|
Sobre las Fractales
|
| En términos generales, una fractal es una ‘una forma geométrica rugosa o fragmentada que puede ser dividida en partes, cada una de las cuales es (al menos de manera aproximada) una copia reducida del total’. Esta propiedad se llama autosemejanza. El término Fractal fue acuñado por Benoît Mandelbrot en 1975, y deriva del latín fractus que significa 'roto' o 'fracturado'. Las fractales se consideran objetos infinitamente complejos, ya que tienen una apariencia similar en todos los niveles de aumento. Algunos fenómenos naturales que se asemejan hasta cierto punto a las fractales son: las nubes, las cordilleras montañosas, los rayos, las líneas costeras y los copos de nieve. |
 |
| Más información sobre fractales
|
 |
 |
 |
 |
 |
| El Conjunto de Mandelbrot es un famoso ejemplo de fractal. |
|
Imagen aumentada del conjunto de Mandelbrot. |
|
 |
| Conjunto de Mandelbrot
|
| El conjunto de Mandelbrot, descubierto en 1980 por Benoît Mandelbrot, es probablemente la fractal más famosa. Como ocurre con los conjuntos de Julia, se genera con una fórmula muy sencilla pero es increíblemente compleja. El conjunto de Mandelbrot es autosimilar de manera aproximada: partes de la fractal original vuelven a aparecer al aumentar la imagen, aunque a menudo aparecen deformadas y con pequeñas diferencias. Esto es lo que hace que aumentar la escala de esta fractal sea tan interesante: uno nunca sabe lo que se va a encontrar. El conjunto de Mandelbrot se genera con la fórmula:zn+1 = zn2 + c donde z y c son números complejos: z = x + iy, z0 = 0, y c es un punto en el plano. La fórmula se repite hasta el momento en el que |zn| (la magnitud de z) sea mayor o igual al valor límite 2. Después, el píxel que corresponde a c se colorea según el número de iteraciones producidas hasta el momento de la finalización del proceso. El área negro de la imagen, es el conjunto de Mandelbrot. Éste consiste de todos los valores de c en los que |zn| no eran mayores de 2. Por supuesto, este área es imposible de calcular de manera precisa, así que el programa colorea de negro todos los píxeles para los que |zn| nunca supera el valor 2 para un número dado de iteraciones, por ejemplo 256. El conjunto Mandelbrot Cúbico se genera con la siguiente fórmula: zn+1 = zn3 + cEl conjunto de Mandelbrot Cuadrático se genera con la siguiente fórmula: zn+1 = zn4 + c
|
 |
| Más información sobre el conjunto de Mandelbrot
|
 |
 |
 |
 |
 |
| Conjunto de Mandelbrot Cúbico |
|
Conjunto de Mandelbrot Cuadrático |
|
 |
| Conjuntos de Julia
|
| Uno de los tipos de fractal más básicos es la familia de los conjuntos de Julia, descubiertos por el matemático francés Gaston Julia durante la primera Guerra Mundial. Los conjuntos de Julia se originan mediante una fórmula muy sencilla con un número complejo llamado C o semilla. Este número puede modificarse para crear muchas variaciones. Los conjuntos de Julia también son autosimilares.
|
 |
| Más información sobre los Conjuntos de Julia
|
 |
 |
| Conjunto de Julia para C = [-0.4, 0.6] |
 |
| Conjuntos de Newton
|
| Esta fractal ha sido generada intentando resolver la ecuación z3 = 1, utilizando el método de Newton-Raphson, donde z es un número complejo: z = x + iy. Esto consiste en definir la función p(z) = z3 - 1, y utilizarla en una fórmula iterativa que devería convergir hacia el cero, encontrando así un valor de z que sea la solución de la primera ecuación. Una generalización de la iteración de Newton es: zn+1 = zn - a * p(zn) / p'(zn) Donde a es cualquier número complejo y p'(z) es la derivada de p(z). La elección especial a = 1 corresponde a la fractal de Newton. Esta fractal aplica la fórmula en cada uno de los puntos del plano complejo, y los colorea en función al número de iteraciones necesarias para que p(z) converja (de manera aproximada) en cero. Las áreas aburridas de la fractal son en realidad soluciones de la ecuación original.
|
 |
| Más información sobre el conjunto de Mandelbrot
|
 |
 |
| Conjunto de Newton para p(z) = z3 - 1, a = 0.5 |
 |
| Dónde empezar
|
| Now that you know a bit more about fractals, you are probably wondering how to produce these with Utimate Fractal. By default, Utimate Fractal opens with a standard Mandelbrot fractal, so the easiest way is to take this fractal and start zooming. Click and drag inside the fractal window to zoom in. Click the right mouse button to zoom out. Ultimate Fractal has many more possibilities, but it is a good idea to start with simple zooming to get a feeling for what fractals are and how Utimate Fractal works.
|
 |
 |
 |
 |
 |
| Pinche y arrastre en la ventana de la fractal para aumentar la imagen. |
|
Sección aumentada de la fractal. |
|
 |
| Parámetros de una Fractal
|
| La ventana Parámetros de la Fractal muestra la posición del centro de la imagen, el número máximo de iteraciones, el grado de aumento o escala, el parámetro complejo C, utilizado para generar el Conjunto de Julia y el parámetro a, utilizado para generar el Conjunto de Newton. Puede modificar todos estos parámetros y pulsar la tecla F5 (Refrescar) o pinchar en el botón Refrescar para ver los resultados.
|
 |
| X |
Valor X del centro de la imagen. Los valores pueden ir de -2 a 2. |
| Y |
Valor Y del centro de la imagen. Los valores pueden ir de -2 a 2. |
| Iteraciones |
El número máximo de iteraciones para generar la fractal. Los valores pueden ir de 1 a 10000. Si el número máximo de iteraciones es demasiado pequeño, los píxeles se colorearán de manera incorrecta (en negro). Por otro lado, si el número de iteraciones es demasiado elevado, se realizarán muchas iteraciones y el tiempo de cálculo de la fractal será mucho mayor. |
| Escala |
El grado de aumento. Un valor de aumento de 200 muestra toda la fractal. |
| X (Julia) |
El valor X del parámetro complejo C, utilizado para generar los Conjuntos de Julia |
| Y (Julia) |
El valor Y del parámetro complejo C, utilizado para generar los Conjuntos de Julia |
| a (Newton) |
El valor del parámetro a, utilizado para generar los Conjuntos de Newton |
|
 |
 |
 |
 |
| La ventana Parámetros de la Fractal muestra la posición del centro de la imagen, el número máximo de iteraciones, el grado de aumento o escala, el parámetro complejo C, utilizado para generar el Conjunto de Julia y el parámetro a, utilizado para generar el Conjunto de Newton. |
 |
| Aumentar y reducir la imagen
|
| Pulse y mantenga presionado el botón izquierdo del ratón y arrastre el cursor dentro de la ventana de la fractal para aumentar la imagen. Pulse el botón derecho del ratón para reducir la imagen. Para modificar la posición de la fractal, seleccione un punto de la fractal pinchando en él con el botón izquierdo del ratón. Este punto se convertirá en el nuevo centro en la ventana de la fractal.
|
 |
 |
El comando Acercar (F9) le permite aumentar la fractal. |
 |
 |
El comando Alejar (F10) le permite reducir la imagen. |
|
 |
| Colores
|
| Los estilos de color definen la manera en la que se colorean las fractales. La fórmula de la fractal crea la forma básica de la misma, mientras que el estilo de color define cómo se colorea esa forma. Esto le da una gran flexibilidad para combinar estilos de color con total libertad en cualquier tipo de fractal. Con Ultimate Fractal puede cambiar entre estilos de color de manera sencilla. Sólo tiene que seleccionar su estilo en el menú Opciones. Puede elegir 4 Colores:
|
 |
| Degradado |
Los píxeles de una fractal se colorean utilizando su índice en un degradado linear. |
| Degradado 3D |
Efecto 3D añadido al estilo Degradado. |
| Variación de Tono |
El componente Tono del píxel es modificado utilizando su valor de índice. |
| Variación de Tono 3D |
Efecto 3D añadido al estilo Variación de Tono |
|
 |
 |
El comando Colores Aleatorios (F6) genera colores aleatorios. |
 |
El comando Editar degradado le permite modificar y cambiar el degradado. |
 |
El comando Abrir degradado abre un degradado (aunque no el resto de parámetros) almacenado en un archivo de parámetros previamente guardado (formato *.fractal). |
|
 |
| El cuadro de diálogo Degradado le permite modificar los valores del degradado. Cambie los colores pinchando en uno de ellos. Mueva las barras para cambiar la posición de los colores de interpolación. La posición de los colores se especifica en porcentajes de distancia a lo largo de la línea de degradado. Por ejemplo, un valor de 20 indica que este punto se encuentra a un 20% del total de la distancia desde el punto de partida. Las posiciones en esta barra están representadas con valores dentre 0 y 100, el primer color en el degradado está en la posición 0 y el último en la posición 100. Marque la casilla Colores Alternos para utilizar dos colores alternos.
|
 |
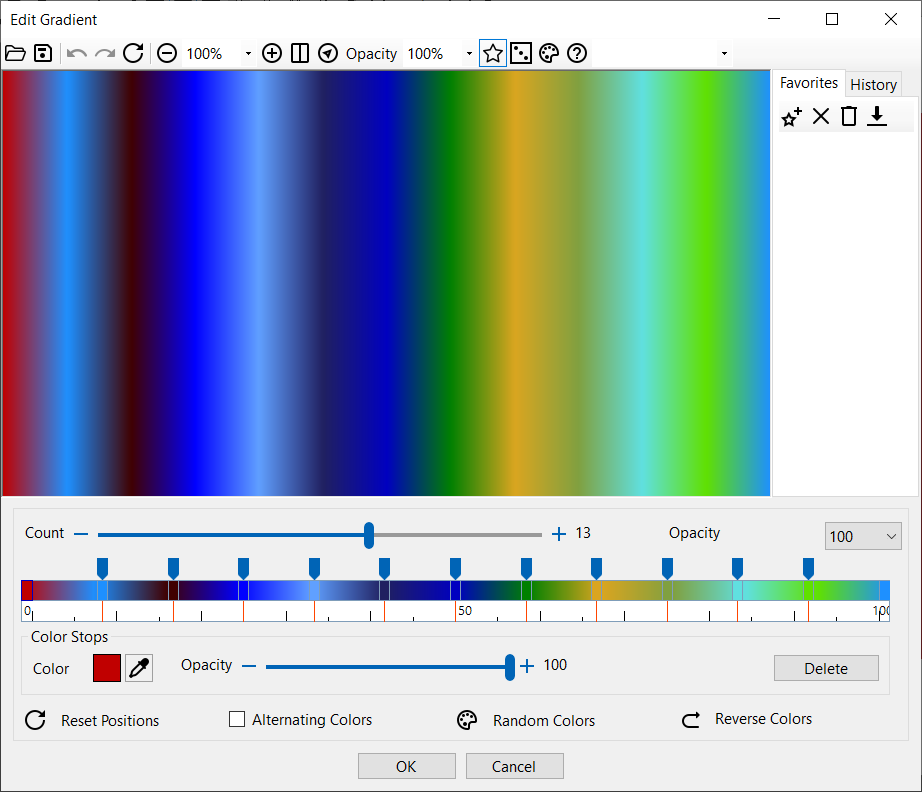 |
| Cuadro de diálogo Degradado |
 |
| Cuando Ultimate Fractal calcula una fractal, no determina un color para cada uno de los píxeles inmediatamente. En lugar de esto, calcula un valor de índice intermedio. Los degradados transforman estos valores de índice en colores. Puesto que sólo se almacenan los índices en los archivos Ultimate Fractal, los colores y el estilo de color pueden modificarse sin tener que calcular la fractal entera. Aquí puede ver un ejemplo de una misma fractal con tres degradados diferentes.
|
 |
|
|
 |
| El menú Archivo contiene los siguientes comandos:
|
 |
El comando Abrir (Ctrl + O) abre un archivo de parámetros previamente guardado (formato *.fractal). |
 |
El comando Guardar parámetros (Ctrl + S) guarda los parámetros de la fractal. Un archivo de fractales contiene una única fractal así como toda la información necesaria para volver a generarla. Los píxeles finales no se almacenan en este archivo. Utilice el comando Guardar Imagen para guardar la fractal en formato de imagen. |
 |
El comando Guardar imagen guarda la fractal en formato de imagen (JPG, PNG, WEBP, GIF, TIF, BMP). |
|
El comando Configurar página le permite establecer las características de la página para su impresión en aplicaciones Windows. |
 |
El comando Imprimir (Ctrl + P) se utiliza para imprimir la fractal. |
|
El comando Vista previa de impresión le permite ver cómo va a quedar la impresión de su fractal. |
|
El comando Archivos recientes le permite abrir una fractal de la lista de archivos recientes. |
|
El comando Salir (Ctrl + Q) le permite cerrar la aplicación. |
|
 |
| El menú Editar contiene los siguientes comandos:
|
 |
El comando Deshacer (Ctrl + Z) deshace la última acción realizada. |
 |
El comando Rehacer (Ctrl + Y) rehace la acción anterior. |
 |
El comando Copiar (Ctrl + C) copia una imagen de la fractal al portapapeles. |
 |
El comando Restablecer (Ctrl + R) restablece los parámetros por defecto de los conjuntos de Mandelbrot o de Julia. |
|
 |
| El menú Vista contiene los siguientes comandos:
|
 |
El comando Acercar (F9) le permite aumentar la fractal. |
 |
El comando Alejar (F10) le permite reducir la imagen. |
 |
El comando Refrescar (F5) le permite actualizar la fractal. |
|
 |
| El menú Opciones contiene los siguientes comandos:
|
 |
El comando Colores Aleatorios (F6) genera colores aleatorios. |
|
El comando Degradados predefinidos le permite elegir un degradado predefinido. |
 |
El comando Editar degradado le permite modificar y cambiar el degradado. |
 |
El comando Abrir degradado abre un degradado (aunque no el resto de parámetros) almacenado en un archivo de parámetros previamente guardado (formato *.fractal). |
 |
El comando Añadir a Favoritos (Ctrl + F) añade los parámetros de la fractal (no el estilo de color o los colores del degradado) a su lista de Favoritos. |
 |
El comando Organizar Favoritos le permite borrar fractales de su lista de Favoritos. |
|
La lista de Favoritos es una manera muy práctica de organizar y acceder a parámetros de fractales que utiliza con frecuencia. Al igual que los marcadores en un explorador de Internet, la lista de Favoritos le ayuda a acceder elementos utilizados muy frecuentemente. Con las fractales de su Lista de Favoritos, puede abrirlas sin tener que explorar todos los archivos de su ordenador. Al abrir un elemento de la lista, se cargan únicamente los parámetros de la fractal, pero no la información de color. Utilice la opción Archivo Abrir para abrir los parámetros de una fractal con su información de color. La carpeta Favoritos está situada en el directorio de la aplicación (C:\Archivos de Programa\Pop Art Studio\Fractals). |
|
 |
| El menú Ayuda contiene los siguientes comandos:
|
 |
El comando Ayuda (F1) muestra la ayuda del programa. |
 |
El comando Idioma le permite cambiar el idioma. |
|
El comando Ordenar le permite comprar el programa en Internet. |
 |
El comando Introducir Clave de Registro le permite escribir su clave de registro y desbloquear el programa. |
 |
El comando Sobre Ultimate Fractal muestra la versión y historia de la misma, la página web y la dirección de correo electrónico de contacto. |
|
 |
| Puede enviar sus preguntas y sugerencias por email a: contact@fotoview.nl.
|