| Ultimate Fractal
|
 |
| Sui frattali |
| L'insieme di Mandelbrot |
| Insiemi di Julia |
| Insiemi di Newton |
| Da dove cominciare |
| Parametri frattali |
| Ingrandire e rimpicciolire |
| Colori |
| Il menu File |
| Il menu Modifica |
| Il menu Visualizza |
| Il menu Opzioni |
| Il menu Aiuto |
 |
|
Sui frattali
|
| Un frattale è generalmente una figura geometrica frammentata che può essere divisa in tante parti, ognuna delle quali rappresenta approssimativamente una copia rimpicciolita del tutto. Questa caratteristica si chiama autosimilarità. Il termine frattale venne coniato nel 1975 da Benoît Mandelbrot, e deriva dal latino fractus. Per il loro aspetto simile a tutti i livelli di grandezza, i frattali sono spesso considerati infinitamente complessi. I frattali possono riprodurre oggetti naturali come nuvole, montagne, fulmini, coste e fiocchi di neve. |
 |
| Ulteriori informazioni sui frattali
|
 |
 |
 |
 |
 |
| L'insieme di Mandelbrot è un famoso esempio di frattale. |
|
Una visualizzazione ravvicinata dell'insieme di Mendelbrot. |
|
 |
| L'insieme di Mandelbrot
|
| L'insieme di Mandelbrot, scoperto nel 1980 da Benoît Mandelbrot, è probabilmente il frattale più famoso. Come per gli insiemi di Julia, esso è generato da una formula molto semplice, e tuttavia rimane un frattale molto complesso. L'insieme di Mandelbrot è vagamente autosimile: parti del frattale originale riappaiono quando lo si ingrandisce; spesso risulta deformato e riporta diversi ornamenti. È proprio questo quello che rende così gratificante guardare l'ingrandimento di questo frattale: non si sa mai cosa si vedrà dopo. L'insieme di Mandelbrot è prodotto dalla formula: zn+1 = zn2 + c dove z e c sono numeri complessi: z = x + iy, y0 = 0, e c è un punto sul piano. La formula viene iterata fino a che |zn| (la grandezza di z) è maggiore o uguale al valore di 2. Quindi, il pixel che corrisponde a c viene colorato in base al numero delle iterazioni che si sono verificate prima che il processo fosse stato salvato. L'area nera dell'immagine priva di interesse è l'effettivo insieme di Mandelbrot. Esso è composto da tutti i valori di c dove |zn| non diventano mai maggiori di 2. Naturalmente è impossibile calcolare accuratamente quest'area, così il programma colora di nero ogni pixel per il quale |zn| non diventa mai maggiore di 2 per un dato numero di iterazioni, ad esempio 256. L'insieme cubico di Mandelbrot è ottenuto dalla funzione: zn+1 = zn3 + c L'insieme quartico di Mandelbrot è prodotto dalla formula: zn+1 = zn4 + c
|
 |
| Ulteriori informazioni sull'insieme di Mandelbrot
|
 |
 |
 |
 |
 |
| L'insieme cubico di Mandelbrot |
|
L'insieme quartico di Mandelbrot |
|
 |
| Insiemi di Julia
|
| Uno dei frattali più basilari è l'insieme di Julia, scoperto durante la prima guerra mondiale dal matematico francese Gaston Julia. Gli insiemi di Julia sono creati da una formula semplice con un parametro complesso chiamato C o seme. Questo parametro può essere modificato in modo da creare diverse variazioni. Gli insiemi di Julia sono anche autosimili.
|
 |
| Ulteriori informazioni sugli insiemi di Julia
|
 |
 |
| L'insieme di Julia per C = [-0.4, 0.6]. |
 |
| Insiemi di Newton
|
| Questo frattale è creato tentando di risolvere l'equazione 3 = 1, usando il metodo Newton-Raphson, dove z è un numero complesso: z = x + iy. Questo comporta il definire la funzione p(z) = z3 - 1, usandola in una formula iterativa che dovrebbe convergere a zero, trovando di conseguenza un valore di z che è la soluzione della prima equazione. Una generalizzazione dell'iterazione di Newton é: zn+1 = zn a* p(zn) / p'(zn) Dove a è qualsiasi numero complesso e p'(z) è la derivata di p(z). La scelta speciale a = 1 corrisponde al frattale di Newton. Questo frattale applica la formula ad ogni punto del piano complesso e lo colora secondo quante iterazioni sono necessarie per far convergere (approssimativamente) p(z) a zero. Le regioni monotone del frattale sono in realtà le soluzioni dell'equazione originale.
|
 |
| Ulteriori informazioni sugli insiemi di Newton
|
 |
 |
| L'insieme di Newton per p(z) = z3 - 1, a = 0.5 |
 |
| Da dove cominciare
|
| Adesso che sapete un po' di più circa i frattali vi state probabilmente chiedendo come crearli con Ultimate Fractal. Ultimate Fractal si apre, in default, con un frattale standard di Mandelbrot. Quindi il modo più facile è prendere questo frattale e ingrandirlo. Cliccare e trascinarlo all'interno della finestra dei frattali per ingrandirlo. Premere il tasto destro del mouse per rimpicciolirlo. Con Ultimate Fractal si hanno molte altre possibilità, ma per avere una prima impressione sui tipi di frattali e su come funziona Ultimate Fractal forse all'inizio sarebbe bene limitarsi ad una semplice zoomata.
|
 |
 |
 |
 |
 |
| Cliccare e trascinare dentro la finestra del frattale da ingrandire. |
|
La parte del frattale ingrandita |
|
 |
| Parametri frattali
|
| La Finestra dei Parametri Frattali mostra il centro display, il numero massimo delle iterazioni, l'ingrandimento o la scala e il complesso parametro C usato nell'insieme di Julia. È possibile cambiare questi parametri e premere F5 (Aggiorna) o il tasto Aggiorna.
|
 |
| X |
Il valore X del centro display. I valori possono andare da -2 a 2. |
| Y |
Il valore Y del centro display. I valori possono andare da -2 a 2. |
| Iterazioni |
Il numero massimo di iterazioni nel calcolo del frattale. Il valori possono andare da 1 a 10000. Se la somma dell'iterazione massima è troppo piccola, il pixel assumerà il colore sbagliato (nero). Di contro, se il conteggio dell'iterazione è troppo grande, saranno create molte iterazioni e il frattale sarà calcolato lentamente. |
| Scala |
L'ingrandimento. Un ingrandimento di 200 volte mostra tutto il frattale. |
| X (Julia) |
Il valore X del parametro C complesso usato nell'insieme di Julia. |
| Y (Julia) |
Il valore Y del parametro C complesso usato nell'insieme di Julia. |
| a (Newton) |
Il valore del parametro a usato nell'insieme di Newton. |
|
 |
 |
 |
 |
| La Finestra dei Parametri Frattali mostra il centro display, il numero massimo delle iterazioni, l'ingrandimento o la scala e il complesso parametro C usato nell'insieme di Julia. |
 |
| Ingrandire e rimpicciolire
|
| Per ingrandire, cliccare, tenere premuto il tasto sinistro del mouse e trascinare dentro la finestra dei frattali. Per rimpicciolire premere il tasto destro del mouse. Per riposizionare il frattale, cliccare il tasto sinistro del mouse per selezionare un punto nel frattale. Questo punto diventerà il nuovo centro nella finestra dei frattali.
|
 |
 |
Il comando Ingrandisci (F9) permette di ingrandire il frattale. |
 |
 |
Il comando Riduci (F10) permette di rimpicciolire il frattale. |
|
 |
| Colori
|
| Uno stile di colore definisce il colore dei frattali. La formula dei frattali crea una forma basilare del frattale, mentre lo stile di colore è un modo di colorare questa forma. Ciò dà la flessibilità di combinare liberamente stili di colori con i diversi frattali. Con Ultimate Fractal è semplice cambiare gli stili di colore. Selezionare lo stile desiderato dal manu Opzioni. Ci sono 4 colori tra cui scegliere:
|
 |
| Gradiente |
I pixel del frattale sono colorati secondo l'indice di valore calcolato in un gradiente lineare. |
| Gradiente 3D |
Effetto 3D aggiunto allo stile Gradiente |
| Variazioni di tonalità |
La componente Tonalità del pixel viene modificata in base all'indice di valore. |
| Variazioni di tonalità 3D |
Effetto 3D aggiunto allo stile Variazione di Tonalità |
|
 |
 |
Il comando Colori Casuali (F6) permette di generare colori casuali. |
 |
Il comando Modifica Gradiente permette di modificare il gradiente. |
 |
Il comando Apri Gradiente apre un gradiente (non gli altri parametri) di un file di parametro precedentemente salvato (*.fractal). |
|
 |
| La finestra di dialogo Gradiente permette di modificare il gradiente. Cambiare i colori cliccando uno dei colori. Trascinare gli slider di posizione per modificare la posizione dei colori di interpolazione. La posizione dei colori nel pannello di controllo specificano la percentuale di distanza lungo la linea di gradiente. Per esempio, un valore di 20 indica che questo punto è il 20 % della distanza totale dal punto di partenza. La posizione in questo pannello di controllo è rappresentata da valori che vanno da 0 a 100, e il primo colore nel gradiente deve essere a posizione 0, mentre l'ultimo deve essere a posizione 100. Selezionare Colori Alternanti per usare due colori che si alternano.
|
 |
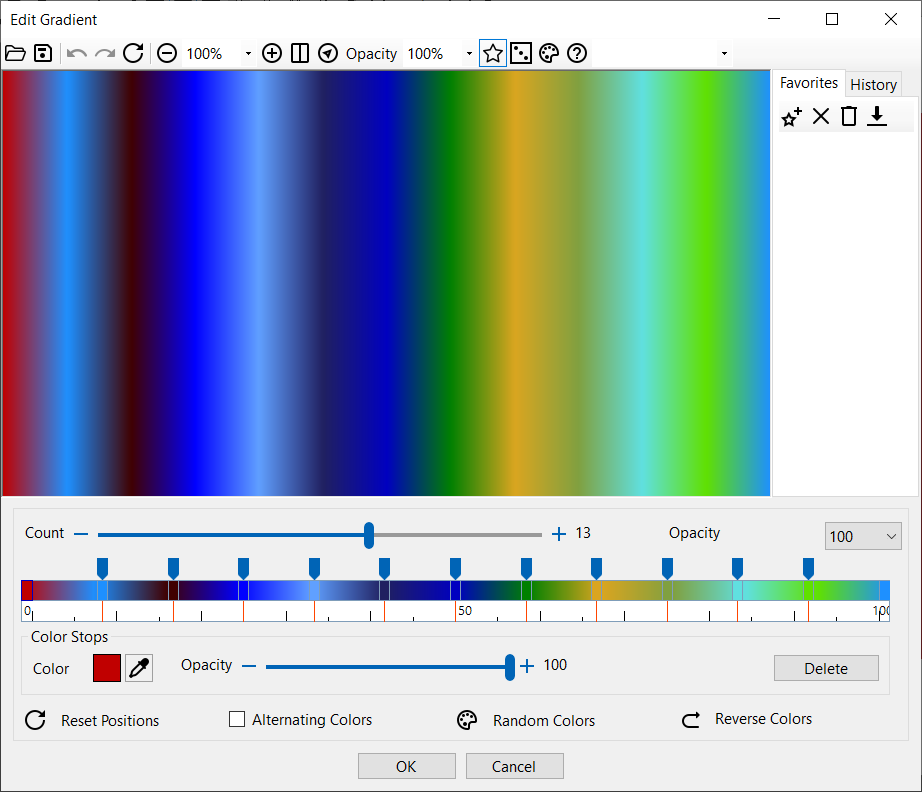 |
| La finestra di dialogo Gradiente |
 |
| Quando Ultimate Fractal calcola un frattale, non calcola immediatamente un colore per ogni pixel, bensì un indice di valore intermedio. Un gradiente traduce valori d'indice in colori. Poiché ad essere salvati sono solo gli indici di valore, i colori e gli stili di colore possono essere modificati senza bisogno di ricalcolare il frattale. Qui c'è un esempio dello stesso frattale con tre diversi gradienti.
|
 |
|
|
 |
| Il menu File contiene le seguenti voci:
|
 |
Il comando Apri (Ctrl + O) apre un file di parametro precedentemente salvato (*.fractal). |
 |
Il comando Salva Parametri (Ctrl + S) salva i parametri frattali. Un file frattale contiene un singolo frattale e tutte le informazioni necessarie per ripristinarlo. I pixel calcolati non vengono salvati. Usare il comando Salva Immagine per salvare il frattale in formato immagine. |
 |
Il comando Salva Immagine salva il frattale in un formato per la rappresentazione di immagini (JPG, PNG, WEBP, GIF, TIF, BMP). |
|
Il comando Impostazione Pagina permette di impostare i parametri della pagina in applicazioni Windows ai fini della stampa. |
 |
Il comando Stampa (Ctrl + P) permette di stampare il frattale |
|
Il comando Anteprima Stampa permette di visualizzare l'anteprima della stampa di un frattale. |
|
Il comando File Recenti permette di aprire un frattale dalla lista dei file recenti. |
|
Il comando Esci (Ctrl + Q) permette di chiudere il programma. |
|
 |
| Il menu Modifica contiene le seguenti voci:
|
 |
Il comando Annulla (Ctrl + Z) permette di annullare l'ultima azione. |
 |
Il comando Ripristina (Ctrl + Y) ripristina l'ultima azione. |
 |
Il comando Copia (Ctrl + C) permette di copiare negli appunti un'immagine del frattale. |
 |
Il comando Azzera (Ctrl + R) permettere di ritornare ai parametri di default di Mandelbrot e Julia. |
|
 |
| Il menu Visualizza contiene le seguenti voci:
|
 |
Il comando Ingrandisci (F9) permette di ingrandire il frattale. |
 |
Il comando Riduci (F10) permette di rimpicciolire il frattale. |
 |
Il comando Annulla (Ctrl + Z) permette di annullare l'ultima azione. |
|
 |
| Il menu Opzioni contiene le seguenti voci:
|
 |
Il comando Colori Casuali (F6) permette di generare colori casuali. |
|
Il comando Gradienti Predefiniti permette di scegliere un gradiente predefinito. |
 |
Il comando Modifica Gradiente permette di modificare il gradiente. |
 |
Il comando Apri Gradiente apre un gradiente (non gli altri parametri) di un file di parametro precedentemente salvato (*.fractal). |
 |
Il comando Aggiungi a Favoriti (Ctrl + F) aggiunge i parametri frattali (e non lo stile di colore, né i colori del gradiente) alla lista dei Favoriti. |
 |
Il comando Ordina Favoriti permette di cancellare dei frattali dalla propria lista dei Favoriti. |
|
La lista dei Favoriti consente di ordinare i parametri frattali usati frequentemente e quindi accedervi con più facilità. Proprio come i segnalibri in un browser, la lista dei Favoriti aiuta ad accedere più velocemente a funzioni utilizzate più frequentemente. Avendo i frattali nella propria lista dei Favoriti, non è necessario caricare il sistema per aprirli. Se si apre un file, verranno aperti solo i parametri frattali e non le informazioni sul colore. Usare il comando Apri File per aprire i parametri frattali incluse le informazioni sul colore. La cartella Favoriti si trova nella directory delle applicazioni (C:\Program Files\Pop Art Studio\Fractals). |
|
 |
| Il menu Aiuto contiene le seguenti voci:
|
 |
Il comando Aiuto (F1) permette di chiedere aiuto. |
 |
Il comando Lingua permette di cambiare lingua. |
|
Il comando Ordina permette di ordinare il programma online. |
 |
Il comando Digita la Chiave di Registrazione permette di digitare la chiave di registrazione e quindi di sbloccare il programma. |
 |
Il comando Informazioni su Ultimate Fractal permette di visualizzare la versione, la storia della versione, il sito internet e l'indirizzo e-mail. |
|
 |
| Per commenti, domande e suggerimenti spedire una e-mail al seguente indirizzo: contact@fotoview.nl.
|